Mahabote algorithm

မနေ့ညက မဟာဘုတ်အတွက် algorithm လေး ရေးကြည့်မယ်ဆိုပြီး စဉ်းစားဖြစ်တယ်။ ကို IT မောင်မောင် တစ်ခေါက်ရေးထားဖူးတယ်။ သို့ပေမယ့် ဘယ်လို စဉ်းစားသွားလဲဆိုတာကို မပါတဲ့ အတွက် algorithm ထွက်လာတာပဲ သိလိုက်တယ်။ ဒါကြောင့် ကိုယ့်ဘာသာကိုယ် စဉ်းစားပြီး algorithm လေး ရေးကြည့်ဖြစ်တယ်။ နောက်ဆုံးထွက်လာတဲ့ algorithm က ကို IT မောင်မောင် နဲ့ မတူဘူးဖြစ်နေတယ်။ သို့ပေမယ့်လည်း အဖြေကတော့ ထွက်တယ်။ IT မောင်မောင် ရေးထားတာ ပိုကောင်းတယ်လို့ ဆိုရမယ်။ ခက်တာက သူ့ website က domain မရှိတော့ဘူး ဖြစ်နေတဲ့အတွက် ကြောင့် ပြန်ညွှန်ပြလို့ မရတော့ဘူး ဖြစ်နေတယ်။ သူရေးခဲ့တာကတော့ တော်တော်ကြာပါပြီ။

ကျွန်တော်တို့ မဟာဘုတ် တွက်တဲ့ အခါမှာ အောင်လံထူစစ်သူကြီးပွဲ ဆိုပြီး မှတ်သားထားတာ ရှိပါတယ်။ ကျွန်တော်ကတော့ ၁ ၄ ၀ ၃ ၆ ၂ ၅ ဆိုပြီးပဲ မှတ်ထားတယ်။

အကြွင်း ၁ အတွက် ဆိုရင် ဒီလို ရလိမ့်မယ်။

    ၅
၀   ၃    ၆
၄   ၁    ၂

အကြွင်း ၂ ဆိုရင်

    ၆
၁   ၄    ဝ
၅   ၂    ၃

အကြွင်း နဲ့ နေ့နံ တွေကို ဇယား ချကြည့်လိုက်ရင် အခုလိုမျိုး ရလာတယ်။

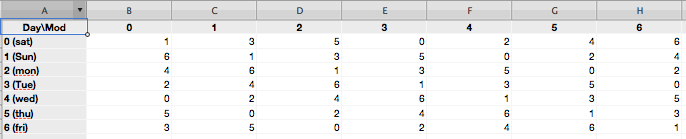
အဲဒီ ဇယားကို ကြည့်လိုက်ရင် အကြွင်းနဲ့ နေ့နံကို ကြည့်တာ နဲ့ ဘာရာသီဖွားလဲဆိုတာကို သိနိုင်ပြီ။

ဥပမာ။။ အကြွင်း ၃ ဗုဒ္ဓဟူးဆိုရင် ၆ ဖြစ်နေတာကို တွေ့မှာပါ။ အဲဒီ နံပတ်တွေက နေရာတွေ ကို ပြောထားတာပါ။

၁ က ဘင်္ဂ
၂ က မရဏ
၃ က အထွန်း
၄ က သိုက်
၅ က ရာဇ
၆ က ပုတိ
၀ က အဓိပတိ

၆ ဆိုတဲ့ အတွက် ပုတိ ။

အဲဒီ ဇယားကို ကြည့်လိုက်ရင် sequence ဖြစ်နေတာကို သတိထားမိလိမ့်မယ်။ ကျွန်တော်တို့ programming မှာ ထည့်သုံးဖို့ အတွက် လွယ်အောင် algorithm ဖန်တီး ဖို့လိုပါတယ်။

ပထမ row တွေ အတိုင်း ရေးချလိုက်ရင်

a0 = 1,3,5,0,2,4,6
a1 = 6,1,3,5,0,2,4
a2 = 4,6,1,3,5,0,2
a3 = 2,4,6,1,3,5,0
a4 = 0,2,4,6,1,3,5
a5 = 5,0,2,4,6,1,3
a6 = 3,5,0,2,4,6,1

ပထမဆုံး row ကို ကျွန်တော် တို့ ကြည့်လိုက်ရင်

1,3,5,7,9 ဆိုတဲ့ sequence နဲ့ ဆင်တာကို ဂရုပြုမိမှာပါ။

1,3,5,7,9……,n sequence ကို algorithm ထုတ်မယ်ဆိုရင်

an = a1 + (n-1)d ဆိုတဲ့ forumla ကို သုံးရပါမယ်။ အဲဒါကို ကျွန်တော်တို့ UCSY third year first term လောက်က သင်ခဲ့ဖူးပါတယ်။

d ဆိုတာကတော့ ခြားနားခြင်းပေါ့။ 1,3,5,7,9 မှာ ခြားနားခြင်းက ၂ ပါ။ a1 ကတော့ ပထမဆုံး ကိန်း နံပတ် ၁ ပါ။

ဒါကြောင့်

an = 1 + (n-1)2
an = 1 + 2n – 2
an = 2n – 1

ဆိုပြီး ထွက်လာပါတယ်။

ဒါကြောင့် ၃ နေရာကို ကြည့်မယ်ဆိုရင်

a3 = 2*3 -1 = 6 -1 = 5

ဆိုပြီး ထွက်ပါတယ်။

1,3,5,7,9,11,13,15 နဲ့ 1,3,5,0,2,4,6 နှိုင်းယှဉ်ကြည့်ရင် 7 နေရာမှာ 0 ကနေ ပြန်စပါတယ်။ ပြီးတော့ အရင်တိုင်း ဆက်ပြီး ပြန်လုပ်ပါတယ်။

ဒါကြောင့် ၇ နဲ့စားပြီး ရတဲ့ အကြွင်းကို ယူပါမယ်။

ဒါကြောင့် ဒီလို ဖြစ်သွားမယ်။

1 Mod 7 , 3 Mod 7 , 5 Mod 7, 7 Mod 7 , 9 Mod 7 , 11 Mod 7

ဆိုရင် ကျွန်တော်တို့လိုချင်တဲ့ 1,3,5,0,2,4,6 ဆိုတာကို ရသွားပါပြီ။

ဆက်ပြီးတော့ ကျွန်တော်တို့မှာ ရှိတဲ့ algorithm ကို apply လုပ်ပါမယ်။

an = (2n – 1) Mod 7

ဆိုရင် မှန်သွားပြီ။ သို့ပေမယ့် ကျွန်တော်တို့က 0 ကနေ စပါတယ်။ ၁ က စတာ မဟုတ်ဘူး။

an = 2*0 – 1 Mod 7 ဆိုရင် မမှန်တောပါဘူး။

ဒါကြောင့် equation က ပြန်ညှိရပါမယ်။ အဖြေ ၁ ထွက်အောင် အတွက် -1 အစား 1 ဖြစ်နေဖို့လိုပါတယ်။ ဒါကြောင့်

an = (2n+1) Mod 7

လို့ ကျွန်တော် ပြင်လိုက်တယ်။

a0 = 1 Mod 7 = 1
a1 = 2+1 Mod 7 = 3
a2 = 4+1 Mod 7 = 5
a3 = 6+1 Mod 7 = 0
a4 = 8+1 Mod 7 = 2
a5 = 10+1 Mod 7 = 4
a6 = 12+1 Mod 7 = 6

ဒါဆိုရင်တော့

an = (2n+1) Mod 7 ဆိုတာ မှန်သွားပြီ။

အဲလိုမျိုးပဲ နေ့နံ ၇ ခုလုံးကို တွက်လိုက်ပါတယ်။ ဒီတော့

a0n = (2n+1) Mod 7
a1n = (2n+6) Mod 7
a2n = (2n+4) Mod 7
a3n = (2n+2) Mod 7
a4n = (2n+0) Mod 7
a5n = (2n+5) Mod 7
a6n = (2n+3) Mod 7

ဆိုပြီး ရလာတယ်။

အဲဒီတော့ series က

(2n+1) Mod 7 , (2n+6) Mod 7 , (2n+4) Mod 7 , (2n+2) Mod 7 , (2n+0) Mod 7 , (2n+5) Mod 7, (2n+3) Mod 7

ဆိုပြီး သတ်မှတ်လို့ရတယ်။ ပထမဆုံးကတော့ စနေ , တနင်္ဂနွေ , တနင်္လာ စသည်ဖြစ် ၇ ခု ရှိပါတယ်။

အဲဒီ မှာ

1,6,4,2,0,5,3 ဆိုတဲ့ sequence ကို တွေ့မှာပါ။

ပုံမှန် ကြည့်လို့ရအောင်

6,4,2,….,n ဆိုပြီး ကြည့်ရအောင်။

တနည်းပြောရင် -2 နှုတ်နှုတ် သွားတာကို တွေ့နိုင်ပါတယ်။

ဒါကြောင့်

an = a1 + (n-1)d
an = 6 + (n-1)-2
an = 6 – 2n + 2
an = 8 – 2n

ဆိုပြီး ရလာတယ်။

1,6,4,2,0,5,3 sequence မှာ တဆင့် ကြည့်ရအောင်။ အရင်လိုပဲ ဂဏန်း ၇ ခု ပတ်နေတဲ့အတွက်ကြောင့် ၇ နဲ့ စားလို့ရတဲ့ အကြွင်းယူပါမယ်။ ဒီတော့

an = (8 – 2n) Mod 7

အဲဒီမှာ ပထမ အခန်းကို ၀ ကနေ စမယ်။

a0 = (8 – 0 ) Mod 7 = 1
a1 = (8 – 2 ) Mod 7 = 6
…
a4 = (8 – 8) Mod 7 = 0

ကဲ ဒါဆိုရင်တော့ အဲဒီ equation မှန်ပြီလို့ ဆိုရမယ်။

အဲဒီတော့

(2n+1) Mod 7 , (2n+6) Mod 7 , (2n+4) Mod 7 , (2n+2) Mod 7 , (2n+0) Mod 7 , (2n+5) Mod 7, (2n+3) Mod 7

ဆိုတဲ့ series မှာ ပေါင်းလိုက်ရင်

[2n+{(8-2k) Mod 7}] Mod 7

ဆိုပြီး ရသွားပါတယ်။ ဒီလို series တွေနဲ့ ပတ်သက်ပြီး စဉ်းစားတာနဲ့ တွက်နည်းတွေကို UCSY third year သင်္ချာမှာ သင်ခဲ့ရတဲ့အတွက် ခက်ခက်ခဲခဲ မဟုတ်ပါဘူး။ အဲဒါက မဟာဘုတ် တွက်ဖို့ အတွက် algorithm ပါပဲ။

n ကတာ့ အကြွင်းပေါ့။ k ကတော့ နေ့နံပေါ့။

ဥပမာ။ ၃ ကြွင်း ၂ (တနင်္လာ) သားသမီးကို ထည့်ပြီး တွက်ကြည့်ရအောင်။

n = 3
k = 2

[2*3 + { (8-2*2) Mod 7 }] Mod 7
[6 + (4 Mod 7)]Mod 7
(6 + 4) Mod 7 = 3

၃ ဖြစ်တဲ့ အတွက် အထွန်းဖွားပါ။

ဒါကြောင့် program ထဲမှာ အဲဒီ equation လေးကို ထည့်လိုက်ရင်ရပါပြီ။

မြန်မာ ခုနှစ် သိရအောင် ဧပြီ ၁၈ မတိုင် ခင်မွေးတဲ့ သူတွေကို ၆၃၉ နှုတ်ပြီး ဧပြီ ၁၈ နောက်ပိုင်း မွေးသူတွေကိုတော့ ၆၃၈ နှုတ်လိုက်ပါ။ ပြီးတော့ ၇ နဲ့ စား ။ ရတဲ့ အကြွင်းကို n နေရာမှာထည့်။ စနေ ဆိုရင် ၀ , တနင်္ဂနွေ ဆိုရင် ၁ ကနေ ပြီးတော့ သောကြာဆိုရင် ၆ ပေါ့။ ဒါကြောင့် မွေးနေ့က k နေရာမှာထည့်လိုက်ရင် ဘာရာသီဖွားလဲဆိုတာကို တွက်နိုင်ပါပြီ။

program ရေးရင် မွေးနေ့ အတိအကျ ထည့်လိုက်တာနဲ့ program ကနေ မွေးတဲ့ နေ့ ပါ ယူလို့ရပါတယ်။ စနေသားလား တနင်္ဂနွေသားလားဆိုတာကို သိနိုင်ပါတယ်။ ပြီးရင် မြန်မာသက္ကရာဇ် ပြန်တွက်။ ၇ နဲ့စား။ ရတာကို

[2n+{(8-2k) Mod 7}] Mod 7

ထဲထည့်ပြီး တွက်လိုက်ရင် ဘာမှ ထွေထွေထူးထူး တွက် စရာမလိုပဲ မဟာဘုတ် ကို သိနိုင်ပါပြီ။

ပိုပြီး လွယ်သွားအောင် နာမည်တွေကို array အခန်းထဲထည့်ထားလိုက်ရင် case စစ်စရာမလိုပဲ ထုတ်လို့ရပါပြီ။

[2n+{(8-2k) Mod 7}] Mod 7 ကို ပိုတိုသွားအောင် ကျွန်တော်တို့တွေ အရင်ဆုံး ဖြန့်ချမယ်။

(2n + 8 Mod 7 – 2k Mod 7) Mod 7

(2n + 1 – 2k Mod 7) Mod 7

2n Mod 7 + 1 Mod 7 – 2k Mod 7

Mod 7 ကို Mod 7 လုပ်ရင် Mod 7 ပဲ ရတယ်။ ဒါကြောင့် (2k Mod 7 ) Mod7 ကနေ 2k Mod 7 ဖြစ်သွားတယ်။

ပြန်ပြီး Mod 7 ကို ဘုံ ထုတ်လိုက်တော့

( 2n + 1 – 2k ) Mod 7

ဖြစ်သွားပြီ။

ဒီထက်ပိုကောင်းတဲ့ နည်းတော့ ရှိမှာ သေချာပါတယ်။ ဒါကြောင့် စာဖတ်သူတွေ အချိန်ရရင်လည်း ကိုယ်တိုင် algorithm တစ်ခုလောက် ထုတ်ကြည့်ပါ။ ကျွန်တော့် algorithm ထက် ပိုကောင်းမှာ သေချာပါတယ်။